SETUP
Test the correctness of this rule by turning over as few cards as possible.
Rule: If the card has a vowel on one side then there is an even number on the other side.
You are then shown four cards with one letter or number printed on the side facing you. The letters and numbers you see are:

The goal is to turn over as few as possible and still test the truth of the rule. So which ones must you turn over?
Resist the temptation to click before deciding. Be bold. Make a choice. No one else will ever know if you were incorrect.
Click here to see the answer when you are ready.
So, how did you do? If you picked the wrong cards you are in good company. 90% of us get it wrong. In fact, when Peter Wason presented this problem in the 1960’s to an audience filled with Ph.D. recipients (many in math and physics) working for IBM they also did very poorly. According to Wason, they were so embarrassed that they harassed him throughout the rest of his lecture claiming the problem was poorly presented.
THE RIGHT CARDS
Most people correctly select the A-card. It makes sense.
Aristotle demonstrated this with the argument form modus ponens.
If p then q
p
Therefore q
For example:
If it rained last night then the grass is wet.
It rained last night.
Therefore the grass is wet.
Very straightforward, right? About 90% of people presented with the card problem get the A-card right. We’re pretty good at spotting this one.
If the card has a vowel on one side then there is an even number on the other side.
The card has a vowel on one side.
Therefore there is an even number on the other side.
If the card does in fact have an even number on the other side then so far so good, otherwise the rule is false.
But what about the other three cards? We don’t do so well. You might even be convinced your answer is correct and I am wrong. Stay with me.
Only about 10% correctly pick the 7-card. Why is this card correct? We’ll use another hypothetical syllogism known as modus tollens.
If p then q
Not q
Therefore not p
A couple of examples:
If it rained last night then the grass is wet.
The grass is not wet.
Therefore it did not rain last night.
If I am out of gas then the car engine is inoperative.
The car engine is not inoperative. (yes, a double-negative but with a purpose)
Therefore I am not out of gas.
The card logic:
If the card has a vowel on one side then there is an even number on the other side.
The card does not have an even number on the other side.
Therefore the card does not have a vowel on one side.
If you turn the 7-card over and see a vowel, you know the rule is not true. Otherwise everything is okay. Anything but a vowel is fair game.
A and 7 (representing modus ponens and modus tollens) are the only cards to test.
Why not the other two?
THE WRONG CARDS
To begin with, the one that trips up about 60% of the people is the 6-card. On the surface it seems to make sense. On the other side it should have a vowel, right? Actually, no. Why? (By the way, this invalid argument form is known within logic as affirming the consequent.)
If p then q
q
Therefore p
For Example:
If it rained last night then the grass is wet.
The grass is wet.
Therefore it rained last night.
Really? Aren’t there plenty of other reasons the grass could be wet? Perhaps a sprinkler system turned on. The neighbors had a water-balloon fight in your yard. Or one million incontinent sky-diving lizards were practicing night jumps over your house. All we know is the grass is wet, but we don’t know why. Sure, if we heard it raining last night then the grass will be wet, but wet grass doesn’t mean rain caused it.
We’re terrible about falling for this.
Superstition uses it:
If the garlic works then I won’t be attacked by a vampire.
I wasn’t attacked by a vampire.
Therefore the garlic works.
Politicians use it:
If taxes are too low then we don’t have enough money for vital public services.
We don’t have enough money for vital public services.
Therefore taxes are too low.
If people have too much of (insert whatever they want to take away from the public) then terrorists/big businesses/criminals will continue to threaten the security of our community.
Terrorists/big businesses/criminals continue to threaten our security of our community.
Therefore people have too much of (insert whatever they want to take away from the public).
That one is especially nasty. Granted, they never put it in exactly those terms, but the underlying logic remains the same. Chris Christie used it a few days ago to justify the actions of the NSA over the last many years. His logic is, since the U.S. hasn’t been attacked this proves the necessity of all the communication data the N.S.A. has been collecting on private citizens. Threats, or lack of threats, do not prove the point. You need to demonstrate a better connection than ‘common sense’ especially when the changes severely impact millions and grants power over the public to servants of the public.
Sure, keeping a life-sized statue of Chewbacca in the bedroom might be keeping the landsharks away, but the fact that you have never had a landshark in your bedroom is not proof that it is necessary. It looks like common sense if you are already convinced it is right. The logic is simply wrong.
This fallacy is one reason science and statistics continually remind us that correlation is not the same thing as causation. We have to fight against the urge to perceive connections when they don’t really exist.
If the card has a vowel on one side then there is an even number on the other side.
There is an even number on the other side.
Therefore the card has a vowel on one side.
Still don’t see the problem?
Assume you turn over the 6-card and discover a Z on it. Would that invalidate the rule? No. The rule said nothing about even numbers always having a vowel on the other side. The rule only says if there is a vowel on one side you will find an even number on the other. Not the reverse. We fall for this logic much too often and unscrupulous people will use it to persuade you to follow their will if you aren’t on guard. Most weeks I can usually spot at least one instance of this in someone’s Facebook posts. Most days you can spot an instance of it within the news.
Finally there is the J-card. Only about 15% want to turn that one over. There is no new information learned if you flip it. The rule says nothing about what is found on the other side of consonant cards. The J-card represents the argument form of denying the antecedent which looks like this.
If p then q
Not p
Therefore not q
For example:
If it rained last night then the grass is wet.
It did not rain last night.
Therefore the grass is not wet.
The grass could still be wet even if it didn’t rain last night. Just like the example above, there are many reasons the grass could be wet. We’ve only ruled out one possible cause.
Again, the rule only claims there are even numbers on the back of vowel-cards. It has nothing to say about consonant cards. Turn it over and you might find an odd number, even number, orange stars, green clovers, or blue diamonds. It doesn’t matter. The validity of the rule isn’t affected by whatever you find on the other side.
In short, the validity of the rule is only affected by what you discover on the other side of the A-card and the 7-card. The other side of the J-card and 6-card is irrelevant.
WHEN WE GET IT RIGHT
On a final note, there is one condition where we perform really well at this. Replace the rule and cards:
Rule: If someone is drinking beer, then the person must be over the age of 21.
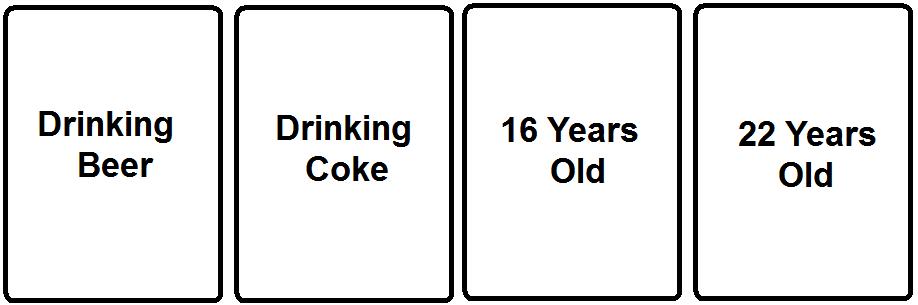
Which cards must you turn over to test this?
Most of us know we should check the age of someone drinking beer (modus ponens) and we need to verify the 16 year old is not drinking beer (modus tollens). So why is this situation different?
Some argue that we have built up a permission schema or cheater detection module based on social expectations. We are disturbed by people abusing social norms. Another possibility is we just have more practice with this rule. Whatever the reason, when Richard Griggs and Julie Cox performed this experiment in 1982, almost 75% of the participants got this one right. That is much better than the 10% who did well in the purely hypothetical situation of letters and numbers.

